Nullspace removal#
The Stokes equation (1) only involves symmetric gradients of the velocity, and as such the velocity is determined only up to rigid-body motions (that is to say, translations and rotations). For many simulations the boundary conditions will fully specify the velocity solution, but for some combinations of geometries and boundary conditions the solution will still be underdetermined. In the language of linear algebra, the Stokes system may have a nullspace.
Usually the user will be able to determine beforehand whether their problem has a nullspace. For instance, a model in a spherical shell geometry with free-slip boundary conditions at the top and bottom will have a rigid-body rotation in its nullspace (but not translations, as the boundary conditions do not allow flow through them). That is to say, the solver may be able to come up with a solution to the Stokes operator, but that solution plus an arbitrary rotation is also an equally valid solution.
Another example is a model in a Cartesian box with periodic boundary conditions in the \(x\)-direction, and free slip boundaries on the top and bottom. This setup has arbitrary translations along the \(x\)-axis in its nullspace, so any solution plus an arbitrary \(x\)-translation is also a solution.
A solution with some small power in these nullspace modes should not affect the physics of the simulation. However, the timestepping of the model is based on evaluating the maximum velocities in the solution, and having unnecessary motions can severely shorten the time steps that ASPECT takes. Furthermore, rigid body motions can make postprocessing calculations and visualization more difficult to interpret.
ASPECT allows the user to specify if their model has a nullspace. If so, any power in the nullspace is calculated and removed from the solution after every timestep. There are two varieties of nullspace removal implemented: removing net linear/angular momentum, and removing net translations/rotations.
For removing linear momentum we search for a constant velocity vector \(\bf c\) such that
This may be solved by realizing that \(\int_\Omega \rho {\bf u} = {\bf p}\), the linear momentum, and \(\int_\Omega \rho = M\), the total mass of the model. Then we find
which is subtracted off of the velocity solution.
Removing the angular momentum is similar, though a bit more complicated. We search for a rotation vector \(\mathbf \omega\) such that
Recognizing that \(\int_\Omega \rho {\bf x \times u} = {\bf H}\), the angular momentum, and \(\int_\Omega \rho {\bf x \times {\mathbf \omega} \times x} = {\bf I \cdot {\mathbf \omega} }\), the moment of inertia dotted into the sought-after vector, we can solve for \({\mathbf \omega}\):
A rotation about the rotation vector \(\omega\) is then subtracted from the velocity solution.
Removing the net translations/rotations are identical to their momentum counterparts, but for those the density is dropped from the formulae. For most applications the density should not vary so wildly that there will be an appreciable difference between the two varieties, though removing linear/angular momentum is more physically motivated.
The user can flag the nullspace for removal by setting the Remove nullspace option, as described in Nullspace removal.
Fig. 1 shows the result of removing angular momentum from a convection model in a 2D annulus with free-slip velocity boundary conditions.
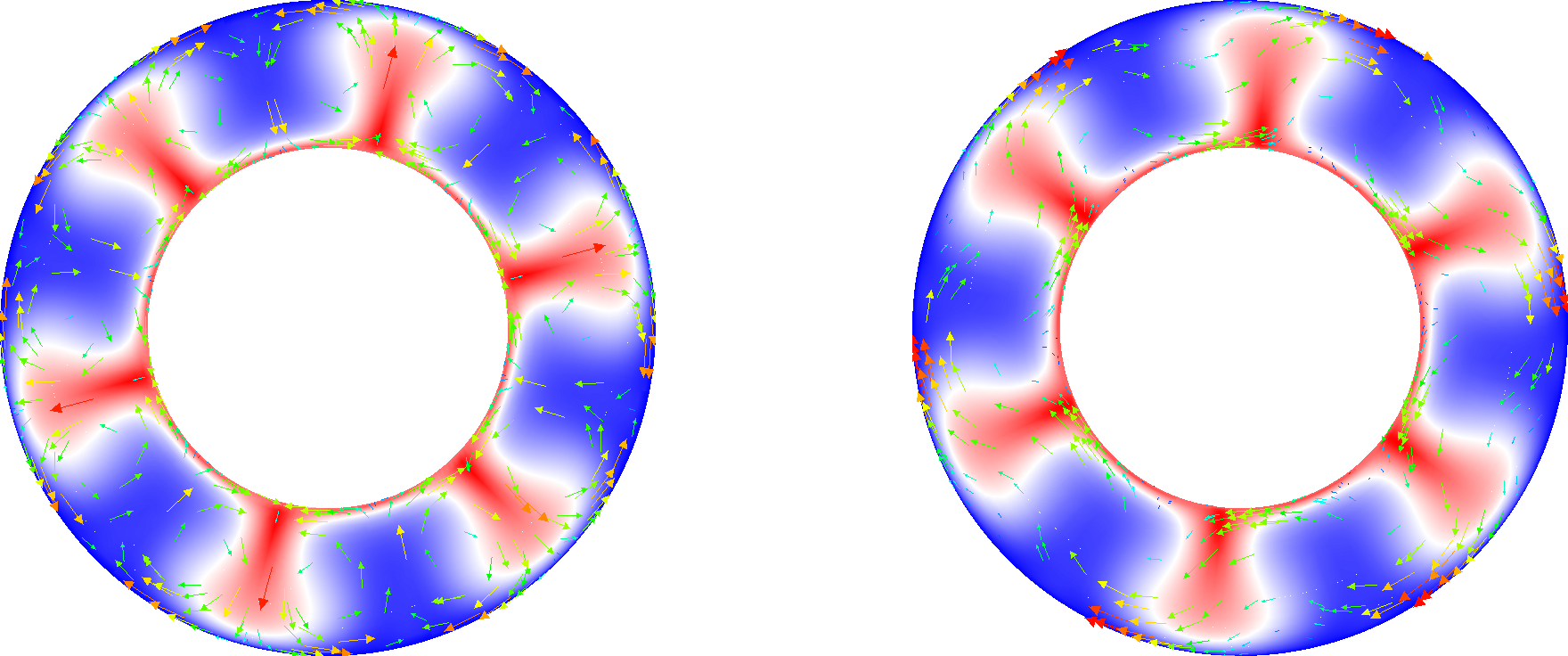
Fig. 1 Example of nullspace removal. On the left the nullspace (a rigid rotation) is removed, and the velocity vectors accurately show the mantle flow. On the right there is a significant clockwise rotation to the velocity solution which is making the more interesting flow features difficult to see.#