2D Lithosphere flexure benchmark with infill#
This section was contributed by D. Douglas.
This model demonstrates ASPECT’s ability to model load induced flexure from a topographic feature on top of the lithosphere. The model uses the viscoelastic material model and is composed of an ‘elastic’ high viscosity lithosphere and a low viscosity mantle beneath the elastic lithosphere. An axisymmetric box load that linearly grows over ten time steps is applied to the top boundary using ASCII files, with the center of the load at the left boundary of the 2D cartesian model domain. The model is run for 120,000 years, which is equivalent to \(40 t_m\), where \(t_m\) is the time scale of viscous stress relaxation for the mantle, and:
\(\eta_m\) is the viscosity of the mantle and \(\mu\) is the elastic shear modulus. This allows for virtually all stresses in the mantle to be relaxed and for the elastic lithosphere to be fully compensating the load. The analytic solution for this setup involves fast fourier transforms and is outlined in the Generic Mapping Tools (GMT) function grdflexure: https://docs.generic-mapping-tools.org/6.1/supplements/potential/grdflexure.html
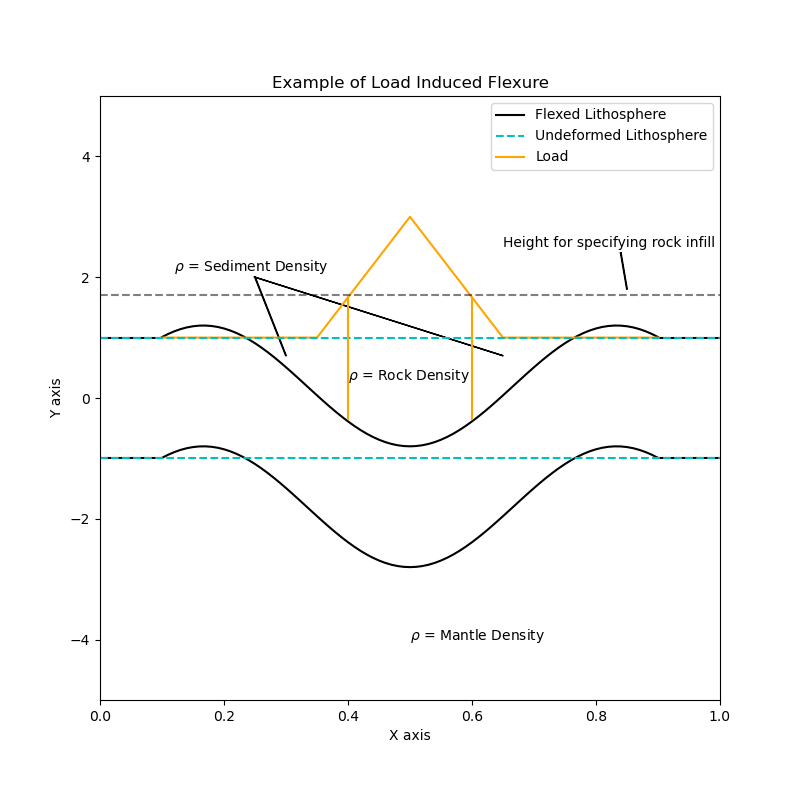
Fig. 227 How infill densities are used in this plugin#
The schematic diagram showing how this plugin works is shown in
Fig. 227. The flexural moat is infilled with either rock or
sediment material based on the parameter Height for specifying rock infill.
It checks if the load at the current point has a height which exceeds the
Height for specifying rock infill. The assumption is that the values taken from
the ASCII file are specifying the part of the load that is above the undeformed
reference surface. If we consider a seamount as the load, the ASCII file takes
the bathymetry of the seamount and provides it as a traction. However, the volcanic
rock comprising the seamount also fills in the flexural moat, providing an additional
traction. Since it is much harder to specify this traction, Height for specifying rock infill
determines where the Rock density that the seamount is made of will infill the
flexural moat, and where Sediment density will infill the flexural moat. For this
test, this variable is not that important given the idealized load, but this is useful
when using more complicated bathymetry maps where small scale seafloor
features makes it unrealistic to set Height for specifying rock infill=0.
As outlined in the GMT documentation, the fourier solution is not valid if the infill density varies spatially, so for this benchmark both infill densities are set to 2000 \(kg/m^3\).
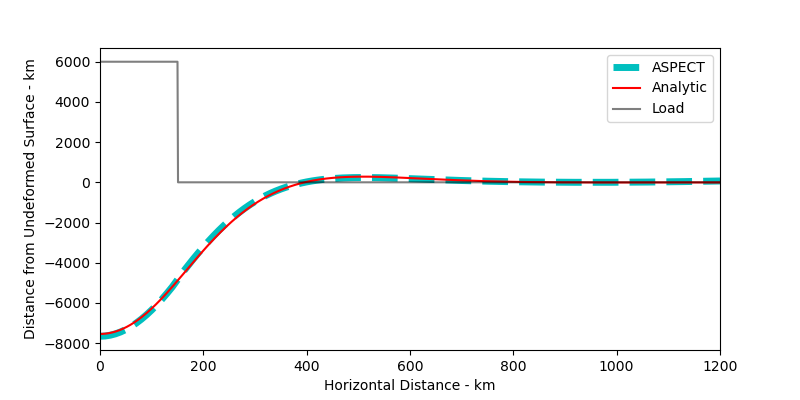
Fig. 228 Comparing ASPECT flexure to analytic solution from GMT. The topographic load is also shown.#
Output from ASPECTs topography postprocessor compared to the analytic solution is shown in Fig. 228. Both the flexural amplitude and the flexural wavelength are accurately recovered.