Viscous inclusions under simple and pure shear

This section was contributed by Cedric Thieulot.

The setup for this experiment originates in Halter et al. [2022]. In the paper the authors present a simple computer program to calculate the stress, pressure, velocity and strain rate fields for two-dimensional (2D) viscous inclusion-matrix systems under pure shear and simple shear.

We here focus on two of their experiments: a strong rectangular inclusion and a weak elliptical inclusion. In both cases the domain is a Cartesian box of size \((L_x,L_y) = (1,1)\) and the magnitude of the applied velocity on the boundaries is 0.5 (this model is formulated in terms of dimensionless quantities). The viscosity of the matrix is set to \(\eta_m=1\), while the viscosity of the inclusion is set to \(\eta_i=1000\) for the rectangular inclusion and \(\eta_i=0.001\) for the elliptical inclusion, see Fig. 127. The setup for the elliptical inclusion is shown in Fig. 128.

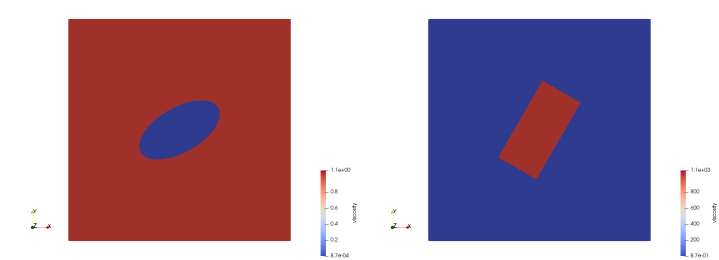
Fig. 127 Viscosity fields for the elliptical and rectangular inclusions.

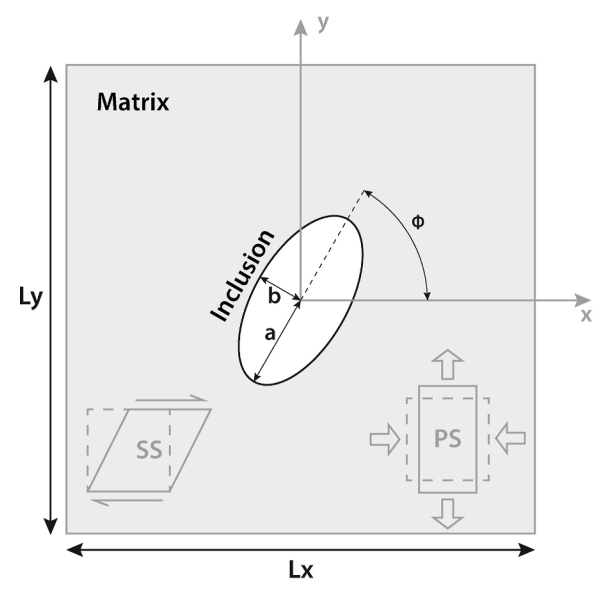
Fig. 128 Model configuration and boundary conditions. An elliptical inclusion of different viscosity than its surrounding matrix is located in the center of a square box of size \(L_x\) by \(L_y\). The ellipse has a semi-major axis \(a\) and semi-minor axis \(b\) and is rotated by angle \(\phi\) from the horizontal axis. Both simple (SS) and pure (PS) shear boundary conditions can be applied. Taken from Halter et al. [2022].

The velocity, pressure and strain rate fields for all four experiments are shown in Fig. 129.

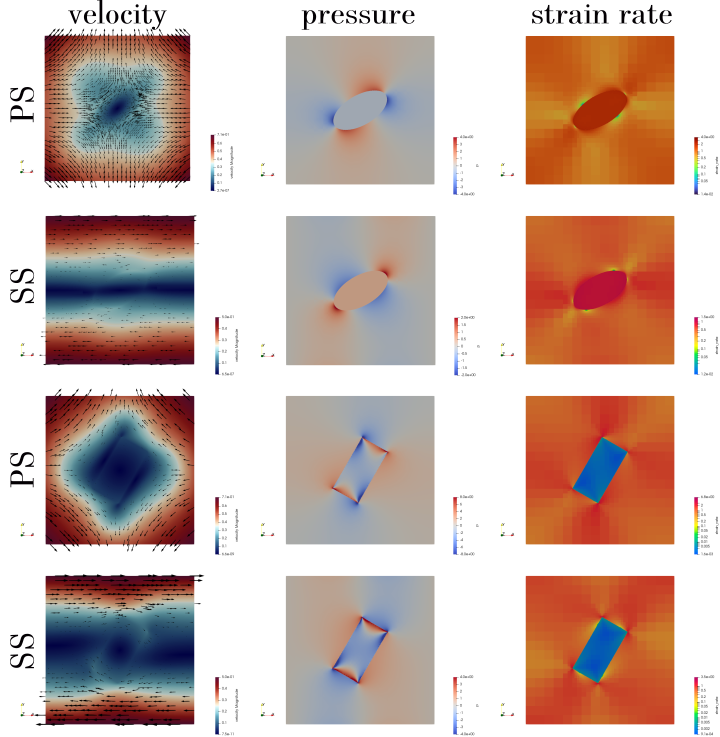
Fig. 129 Results for both inclusion types and both boundary condition types. ‘SS’ stands for simple shear and ‘PS’ stands for pure shear.

In the paper the authors also look at the case of a power-law rheology for the matrix. Instead of trying to reproduce their results exectly, let us simply create a test case for such an experiment. We then replace the simple material model by the Visco Plastic material model, select the dislocation creep flow law, set the activation volume and activation energy to zero, and set the cohesion to a very large value so that plastic behavior is never triggered. In the end the effective viscosity is then given by:

\[\eta = \frac12 A^{-1/n} \dot\varepsilon_e\]

If \(n=1\) then the viscosity is Newtonian, i.e. \(\eta=\frac12 A^{-1}\), and by taking \(A=500\) then we ensure that the inclusion has a constant viscosity \(\eta_i=0.001\) as before. Concerning the matrix, we set \(A=0.5\) so that when \(n=1\) we recover \(\eta_m=1\). In Fig. 130 results obtained with \(n=1,2,3\) are shown.

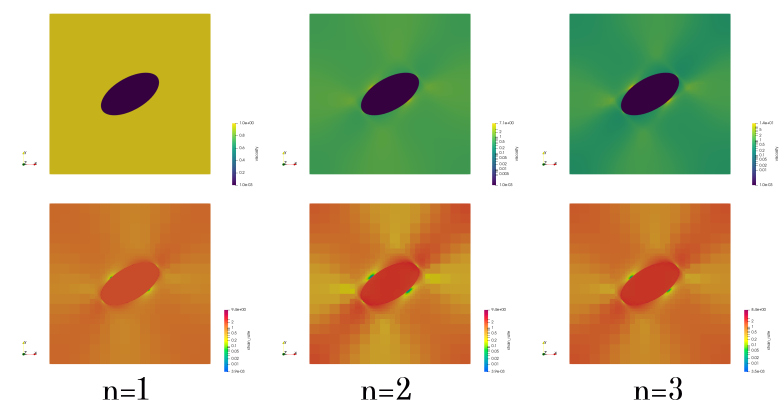
Fig. 130 Results for an elliptical inclusion under pure shear with a power-law rheology for the matrix with \(n=1,2,3\).