The Burstedde variable viscosity benchmark#
This section was contributed by Iris van Zelst.
This benchmark is intended to test solvers for variable viscosity Stokes problems. It begins with postulating a smooth exact polynomial solution to the Stokes equation for a unit cube, first proposed by Dohrmann and Bochev [2004] and also described by Burstedde et al. [2013]:
It is then trivial to verify that the velocity field is divergence-free. The constant \(-\frac{5}{32}\) has been added to the expression of \(p\) to ensure that the volume pressure normalization of can be used in this benchmark (in other words, to ensure that the exact pressure has mean value zero and, consequently, can easily be compared with the numerically computed pressure). Following Burstedde et al. [2013], the viscosity \(\mu\) is given by the smoothly varying function
The maximum of this function is \(\mu = e\), for example at \((x,y,z)=(0,0,0)\), and the minimum of this function is \(\mu = \exp \Big( 1-\frac{3\beta}{4}\Big)\) at \((x,y,z) = (0.5,0.5,0.5)\). The viscosity ratio \(\mu^\ast\) is then given by
Hence, by varying \(\beta\) between 1 and 20, a difference of up to 7 orders of magnitude viscosity is obtained. \(\beta\) will be one of the parameters that can be selected in the input file that accompanies this benchmark.
The corresponding body force of the Stokes equation can then be computed by inserting this solution into the momentum equation,
Using equations (37), (38) and (39) in the momentum equation (40), the following expression for the body force \(\rho\mathbf g\) can be found:
Assuming \(\rho = 1\), the above expression translates
into an expression for the gravity vector \(\mathbf g\). This expression for the
gravity (even though it is completely unphysical), has consequently been
incorporated into the BursteddeGravity gravity model that is described in
the benchmarks/burstedde/burstedde.cc file that accompanies this benchmark.
We will use the input file benchmarks/burstedde/burstedde.prm as input,
which is very similar to the input file benchmarks/inclusion/adaptive.prm
discussed above in The “inclusion” Stokes benchmark. The major
changes for the 3D polynomial Stokes benchmark are listed below:
subsection Solver parameters
subsection Stokes solver parameters
set Linear solver tolerance = 1e-12
end
end
# Boundary conditions
subsection Boundary velocity model
set Prescribed velocity boundary indicators = left : BursteddeBoundary, \
right : BursteddeBoundary, \
front : BursteddeBoundary, \
back : BursteddeBoundary, \
bottom: BursteddeBoundary, \
top : BursteddeBoundary
end
subsection Material model
set Model name = BursteddeMaterial
end
subsection Gravity model
set Model name = BursteddeGravity
end
subsection Burstedde benchmark
# Viscosity parameter is beta
set Viscosity parameter = 20
end
subsection Postprocess
set List of postprocessors = visualization, velocity statistics, BursteddePostprocessor
end
The boundary conditions that are used are simply the velocities from equation
(37) prescribed on each boundary. The viscosity
parameter in the input file is \(\beta\). Furthermore, in order to compute the
velocity and pressure \(L_1\) and \(L_2\) norm, the postprocessor
BursteddePostprocessor is used. Please note that the linear solver tolerance
is set to a very small value (deviating from the default value), in order to
ensure that the solver can solve the system accurately enough to make sure
that the iteration error is smaller than the discretization error.
Expected analytical solutions at two locations are summarised in Table 9 and can be deduced from equations (37) and (38). Fig. 184 shows that the analytical solution is indeed retrieved by the model.
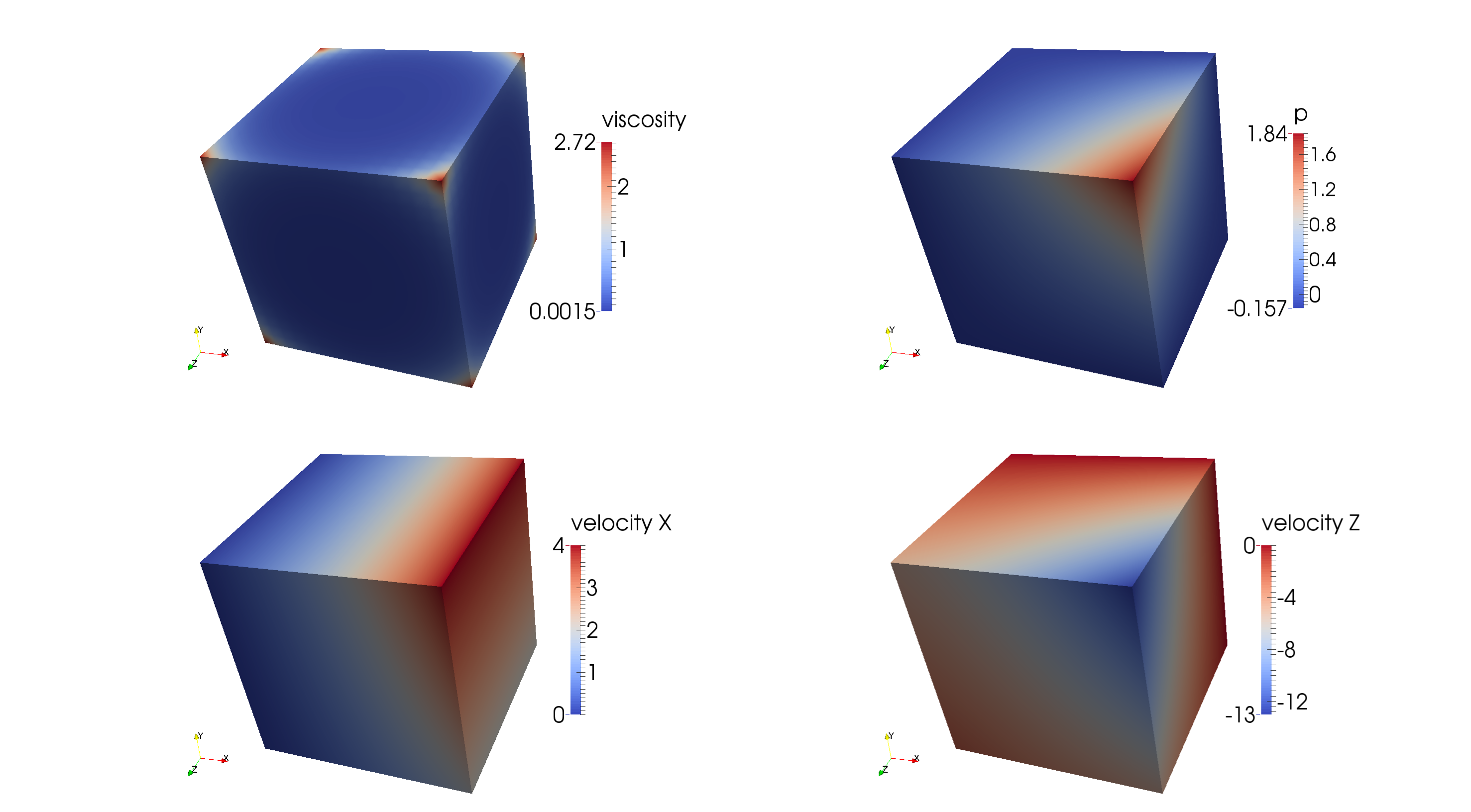
Fig. 184 Burstedde benchmark: Results for the 3D polynomial Stokes benchmark, obtained with a resolution of \(16\times 16\) elements, with \(\beta = 10\).#
Quantity |
\(\mathbf{r} = (0,0,0)\) |
\(\mathbf{r} = (1,1,1)\) |
|---|---|---|
\(p\) |
\(-0.15625\) |
\(1.84375\) |
\(\mathbf{u}\) |
\((0,0,0)\) |
\((4,4,-13)\) |
\(|\mathbf{u}|\) |
\(0\) |
\(14.177\) |
The convergence of the numerical error of this benchmark has been analysed by playing with the mesh refinement level in the input file, and results can be found in Fig. 185. The velocity shows cubic error convergence, while the pressure shows quadratic convergence in the \(L_1\) and \(L_2\) norms, as one would hope for using \(Q_2\) elements for the velocity and \(Q_1\) elements for the pressure.
Fig. 185 Burstedde benchmark: Error convergence for the 3D polynomial Stokes benchmark.#