Melt migration in a 2D mantle convection model#
This section was contributed by Juliane Dannberg and is based on a section in Dannberg and Heister [2016] by Juliane Dannberg and Timo Heister.
The following cookbook will explain how to use ASPECT’s implementation of coupled magma/mantle dynamics (see Calculations with melt transport) to set up a model of mantle convection that also includes melting and freezing of mantle rock, and the transport of melt according to the two-phase flow equations. The model setup is described in detail in Dannberg and Heister [2016], which can be found here, and in the following we will go over a slightly simplified version in lower resolution. We will start by looking at a global mantle convection without melt migration, and will then discuss how the input file has to be modified in order to add melt transport. A movie that compares the evolution of the temperature field and the amount of melt present in both models in higher resolution can be found online.
The model setup is a 2D box with dimensions of \(2900 \times 8700\) km,
and it is heated from the bottom and cooled from the top. A full description
can be found in Section 4.7 “Influence of melt migration on a
global-scale convection model” in Dannberg and Heister [2016]. In the
first model we will look at, melting and freezing is only included passively:
We use the melt fraction visualization postprocessor to compute how much
melt is present for a given temperature and pressure at every given point in
time and space in our model, but the presence of melt does not influence
material properties like density or viscosity, and melt does not move relative
to the solid. This also means that because melt is not extracted, the bulk
composition of the material always stays the same, and melt only freezes again
once advection or conduction causes the temperature of the solid rock to be
below the solidus. The following input file (which can be found in
cookbooks/global_melt/global_no_melt.prm) contains a detailed description
of the different options required to set up such a model:
# Model setup for mantle convection in a 2D box without melting.
# This file is used as a starting point for a cookbook that
# explains how to add melting and melt transport to a mantle
# convection simulation.
set Dimension = 2
set Adiabatic surface temperature = 1600
set Maximum time step = 1e6
set Output directory = output-global_no_melt
set Use years in output instead of seconds = true
# The end time of the simulation. Because we want to see how upwellings
# and downwellings evolve over time, and if differences develop between
# the model with and without melt migration, we set the end time to 200 Ma.
set End time = 2e8
# We choose a stricter than default linear Stokes solver tolerance,
# to be consistent with the global_melt cookbook.
subsection Solver parameters
subsection Stokes solver parameters
set Linear solver tolerance = 1e-8
set Number of cheap Stokes solver steps = 100
end
end
# We prescribe free-slip boundary conditions on all
# sides.
subsection Boundary velocity model
set Tangential velocity boundary indicators = left, right, top, bottom
end
# We also choose relatively large values for the stabilization parameters:
# The model resolution is very coarse (in order for this model to run in a
# short time), so we want to make sure that no temperature over- and
# undershoots will develop. In a model with melting this would be
# particularly problematic, as large amounts of melt could be generated
# by temperature spikes, and we want to be consistent between the model
# with and without melt transport.
subsection Discretization
subsection Stabilization parameters
set beta = 0.5
set cR = 1
end
end
##################### Initial conditions ########################
# We choose an adiabatic temperature profile as initial condition,
# with conductive temperature profiles in the top and bottom boundary
# layers, which were computed using a half space cooling model.
# The cold top boundary layer corresponds to an age of 70 Ma,
# and the hot top boundary layer corresponds to an age of 700 Ma.
# A small temperature perturbation is added at the bottom of the
# domain. To make the model asymmetric, we place it in a distance of
# x = 2900 km from the left boundary.
# Temperatures from both initial temperature models we specify are
# added (by default).
subsection Initial temperature model
set List of model names = adiabatic, function
subsection Adiabatic
set Age bottom boundary layer = 7e8
set Age top boundary layer = 7e7
subsection Function
set Function expression = 0;0
end
end
subsection Function
set Function constants = r=350000, amplitude=50
set Function expression = if((x-2900000)*(x-2900000)+y*y<r,amplitude,0)
end
end
##################### Boundary conditions ########################
# As boundary conditions for the temperature, we just use the
# initial conditions again. This temperature is applied as a prescribed
# temperature at the top and bottom boundary.
subsection Boundary temperature model
set Fixed temperature boundary indicators = top, bottom
set List of model names = initial temperature
subsection Initial temperature
set Minimal temperature = 293
set Maximal temperature = 3900
end
end
##################### Model geometry ########################
# The model geometry is a box with an aspect ratio of 3,
# extending to the base of the mantle in vertical direction.
subsection Geometry model
set Model name = box
subsection Box
set X extent = 8700000
set Y extent = 2900000
set X repetitions = 3
end
end
################ Gravity and material properties ##################
# The model has a constant gravity.
subsection Gravity model
set Model name = vertical
subsection Vertical
set Magnitude = 9.81
end
end
# We use the melt global material model, which is one of the
# material models that works with melt transport, as it also
# specifies the material properties needed for melt migration,
# such as the permeability, the melt density and the melt
# viscosity.
# It also works without melt transport, and in this case these
# properties are not used, so we do not have to specify them
# here.
subsection Material model
set Model name = melt global
subsection Melt global
set Thermal conductivity = 4.7
set Reference solid density = 3400
set Thermal expansion coefficient = 2e-5
set Reference shear viscosity = 5e21
set Thermal viscosity exponent = 7
set Reference temperature = 1600
set Solid compressibility = 4.2e-12
end
end
##################### Mesh refinement #########################
# For the model without melt migration, we do not have to use
# mesh adaptivity, because time- and length scales of material
# motion does do not vary a lot across the model, and a global
# resolution of 5 is sufficient to capture the behavior of
# upwellings and downwellings. We nevertheless want to refine
# the mesh near the top and bottom boundaries where large
# thermal gradients occur.
subsection Mesh refinement
set Initial adaptive refinement = 2
set Initial global refinement = 5
set Strategy = minimum refinement function, boundary
set Time steps between mesh refinement = 0
# minimum of 5 global refinements
subsection Minimum refinement function
set Function expression = 5
end
# refine at top and bottom boundary
subsection Boundary
set Boundary refinement indicators = top, bottom
end
end
# As the model is compressible and has an adiabatic temperature profile, we include
# adiabatic heating in the list of heating models.
# To make this model as simple as possible, we do not include shear heating (although
# usually, adiabatic heating and shear heating should always be used together).
subsection Heating model
set List of model names = adiabatic heating
end
##################### Postprocessing ########################
# In addition to the visualization output, we select a number
# of postprocessors that allow us to compute some statistics
# about the output (to see how much the model without and the
# model with melt migration differ), and in particular we use
# the "depth average" postprocessor that will allow us to plot
# depth-averaged model quantities over time.
subsection Postprocess
set List of postprocessors = visualization, composition statistics, velocity statistics, temperature statistics, melt statistics, depth average
# For the model without melt migration, we only compute the
# equilibrium melt fraction in dependence of temperature and
# pressure. This is done as a postprocessing step, by adding
# "melt fraction" to the list of material properties in the
# corresponding visualization postprocessor.
subsection Visualization
set List of output variables = material properties, nonadiabatic temperature
set Number of grouped files = 0
set Output format = vtu
set Time between graphical output = 6e5
subsection Material properties
set List of material properties = density, viscosity, melt fraction
end
end
subsection Depth average
set Number of zones = 12
set Time between graphical output = 6e5
end
end
# We write a checkpoint approximately every half an hour,
# so that we are able to restart the computation from that
# point.
subsection Checkpointing
set Time between checkpoint = 1700
end
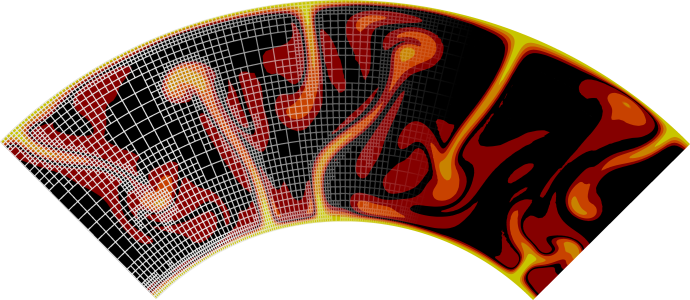
When we look at visualization output of this model, we can see that over time, first upwellings, and then downwellings start to form. Both are more or less stable over time, and only change their positions slowly. As melt does not move relative to the solid, broad stable zones of melting with melt fraction of 10% or more form in areas where material is upwelling.
In the second model, melt is an active component of the model. Temperature,
pressure and composition control how much of the rock melts, and as soon as
that happens, melt can migrate relative to the solid rock. As material only
melts partially, that means that the composition of the rock changes when it
melts and melt is extracted, and we track this change in composition using a
compositional field with the name peridotite. Positive values mark depletion
(the composition of the residual host rock as more and more melt is
extracted), and negative values mark enrichment (the composition of generated
melt, or regions where melt freezes again). Both the fraction of melt (tracked
by the compositional field with the name porosity) and the changes in
composition influence the material properties such as density and viscosity.
Moreover, there are additional material properties that describe how easily
melt can move through the host rock, such as the permeability, or properties
of the melt itself, such as the fluid viscosity. The following input file (a
complete version of which can be found in
cookbooks/global_melt/global_melt.prm) details the changes we have to make
from the first model to set up a model with melt migration:
# Cookbook for a global-scale 2D box mantle convection model
# with melt migration.
# In this file we will go through all of the steps that are
# required for adding melting and melt transport to a mantle
# convection simulation.
# For models with melt migration, there is a nonlinear coupling between
# the Stokes system, the temperature, and the advection equation for the
# porosity (several material properties, such as the viscosities and the
# permeability depend nonlinearly on the porosity; and changes in temperature
# determine how much material is melting or freezing).
# Because of that, we use a nonlinear solver scheme ('iterated Advection and Stokes')
# that iterates between all of these equations, and we have to set its
# solver tolerance and the maximum number of iterations separately from
# the linear solver parameters.
set Nonlinear solver scheme = iterated Advection and Stokes
set Max nonlinear iterations = 20
set Nonlinear solver tolerance = 1e-5
# In addition, melting and freezing normally happens on a much faster
# time scale than the flow of melt, so we want to decouple the advection
# of melt (and temperature) and the melting process itself. To do that,
# we use the operator splitting scheme, and define that for every
# advection time step, we want to do at least 10 reaction time steps.
# If these time steps would be larger than 10,000 years, we will do
# more reaction time steps (so that reaction time step size never exceeds
# 10,000 years). Here, we also specify the Stokes linear solver tolerance
# and maximum number of cheap Stokes solver steps to improve the nonlinear
# convergence behavior.
set Use operator splitting = true
subsection Solver parameters
subsection Operator splitting parameters
set Reaction time step = 1e4
set Reaction time steps per advection step = 10
end
subsection Stokes solver parameters
set Linear solver tolerance = 1e-8
set Number of cheap Stokes solver steps = 100
end
end
subsection Melt settings
# In addition, we now also specify in the model settings that we want to
# run a model with melt transport.
set Include melt transport = true
end
##################### Settings for melt transport ########################
# In models with melt transport, we always need a compositional field with
# the name 'porosity'. Only the field with that name will be advected with
# the melt velocity, all other compositional fields will continue to work
# as before. Material models will typically query for the field with the
# name porosity to compute all melt material properties.
# In addition, the 'melt global' material model also requires a field with the
# name 'peridotite'. This field is used to track how much material has been
# molten at each point of the model, so it tracks the information how the
# composition of the rock changes due to partial melting events (sometimes
# also called depletion). This is important, because usually less melt is
# generated for a given temperature and pressure if the rock has undergone
# melting before. Typically, material properties like the density are also
# different for more or less depleted material.
subsection Compositional fields
set Number of fields = 2
set Names of fields = porosity, peridotite
end
##################### Initial conditions ########################
# Now that our model uses compositional fields, we also need initial
# conditions for the composition.
# We use the function plugin to set both fields to zero at the beginning
# of the model run.
subsection Initial composition model
set Model name = function
subsection Function
set Function expression = 0; 0
set Variable names = x,y
end
end
##################### Boundary conditions ########################
# We again choose the initial composition as boundary condition
# for all compositional fields.
subsection Boundary composition model
set List of model names = initial composition
end
# Models with melt transport also need an additional boundary condition:
# the gradient of the fluid pressure at the model boundaries. This boundary
# condition indirectly also prescribes boundary conditions for the melt velocity,
# as the melt velocity is related to the fluid pressure gradient via Darcy's law.
# If we choose the fluid pressure gradient = solid density * gravity, melt will
# flow in and out of the model (even if the solid can not flow out) according to
# the dynamic fluid pressure in the model. Conversely, if we choose the
# fluid pressure gradient = fluid density * gravity, melt will flow in or out
# with the same velocity as the solid (so for a closed boundary, no melt will
# flow in or out). This is what we choose as our boundary condition here.
subsection Boundary fluid pressure model
set Plugin name = density
subsection Density
set Density formulation = fluid density
end
end
##################### Material properties ########################
# In addition to the material properties for the solid rock,
# we also have to specify properties for the melt.
subsection Material model
set Model name = melt global
subsection Melt global
# First we describe the parameters for the solid, in the same way
# we did in the model without melt transport
set Thermal conductivity = 4.7
set Reference solid density = 3400
set Thermal expansion coefficient = 2e-5
set Reference shear viscosity = 5e21
set Thermal viscosity exponent = 7
set Reference temperature = 1600
set Solid compressibility = 4.2e-12
# The melt usually has a different (lower) density than the solid.
set Reference melt density = 3000
# The permeability describes how well the pores of a porous material
# are connected (and hence how fast melt can flow through the rock).
# It is computed as the product of the reference value given here
# and the porosity cubed. This means that the lower the porosity is
# the more difficult it is for the melt to flow.
set Reference permeability = 1e-8
# The bulk viscosity describes the resistance of the rock to dilation
# and compaction. Melt can only flow into a region that had no melt
# before if the matrix of the solid rock expands, so this parameter
# also limits how fast melt can flow upwards.
# The bulk viscosity is computed as the reference value given here times
# a term that scales with one over the porosity. This means that for zero
# porosity, the rock can not dilate/compact any more, which is the same
# behavior that we have for solid mantle convection.
set Reference bulk viscosity = 1e19
# In dependence of how much melt is present, we also weaken the shear
# viscosity: The more melt is present, the weaker the rock gets.
# This scaling is exponential, following the relation
# viscosity ~ exp(-alpha * phi),
# where alpha is the parameter given here, and phi is the porosity.
set Exponential melt weakening factor = 10
# In the same way the shear viscosity is reduced with increasing temperature,
# we also prescribe the temperature-dependence of the bulk viscosity.
set Thermal bulk viscosity exponent = 7
# Analogous to the compressibility of the solid rock, we also define a
# comressibility for the melt (which is generally higher than for the solid).
# As we do not want our compressibility to depend on depth, we set the
# pressure derivative to zero.
set Melt compressibility = 1.25e-11
set Melt bulk modulus derivative = 0.0
# Finally, we prescribe the viscosity of the melt, which is used in Darcy's
# law. The lower this viscosity, the faster melt can flow.
set Reference melt viscosity = 1
# change the density contrast of depleted material (in kg/m^3)
set Depletion density change = -200.0
# How much melt has been generated and subsequently extracted from a particular
# volume of rock (how 'depleted' that volume of rock is) usually changes the
# solidus. The more the material has been molten already, the less melt will be
# generated afterwards for the same pressure and temperature conditions. We
# model this using a simplified, linear relationship, saying that to melt 100%
# of the rock the temperature has to be 200 K higher than to melt it initially.
set Depletion solidus change = 200
# We also have to determine how fast melting and freezing should happen.
# Here, we choose a time scale of 10,000 years, which is a relatively long time
# (or in other words, slow melting rate), but because this is a global model
# and the time steps are big, it should be sufficient.
set Melting time scale for operator splitting = 1e4
end
end
##################### Mesh refinement #########################
# For the model with melt migration, we use adaptive refinement.
# We make use of two different refinement criteria: we set a minimum of 5 global
# refinements everywhere in the model (which is the same resolution as for the
# model without melt), and we refine in regions where melt is present, to be
# precise, everywhere where the porosity is bigger than 1e-6.
# We adapt the mesh every 5 time steps.
subsection Mesh refinement
set Coarsening fraction = 0.05
set Refinement fraction = 0.8
set Initial adaptive refinement = 2
set Initial global refinement = 5
set Strategy = composition threshold, minimum refinement function, boundary
set Time steps between mesh refinement = 5
# minimum of 5 global refinements
subsection Minimum refinement function
set Function expression = 5
end
# refine where the porosity is bigger than 1e-6
subsection Composition threshold
set Compositional field thresholds = 1e-6,1.0
end
# refine at top and bottom boundary
subsection Boundary
set Boundary refinement indicators = top, bottom
end
end
##################### Postprocessing ########################
# In addition to the visualization output, we select a number
# of postprocessors that allow us to compute some statistics
# about the output (to see how much the model without and the
# model with melt migration differ), and in particular we use
# the "depth average" postprocessor that will allow us to plot
# depth-averaged model quantities over time.
subsection Postprocess
set List of postprocessors = visualization, composition statistics, velocity statistics, temperature statistics, depth average
# For the model with melt migration, also add a visualization
# postprocessor that computes the material properties relevant
# to migration (permeability, viscosity of the melt, etc.).
subsection Visualization
set List of output variables = material properties, nonadiabatic temperature, strain rate, melt material properties
subsection Material properties
set List of material properties = density, viscosity, thermal expansivity
end
subsection Melt material properties
set List of properties = fluid density, permeability, fluid viscosity, compaction viscosity
end
end
end
In the first few tens of millions of years, this models evolves similarly to the model without melt migration. Upwellings rise in the same locations, and regions where material starts to melt are similar. However, once melt is formed, the model evolutions start to deviate. In the model with melt migration, melt moves upwards from the region where it is generated much faster than the flow of solid material, so that it reaches cold regions – where it freezes again – in a shorter amount of time. Because of that, the overall amount of melt is smaller in this model at any given point in time. In addition, enriched material, present in places where melt has crystallized, has a higher density than average or depleted mantle material. This means that in regions above stable upwellings, instabilities of dense, enriched material start to form, which leads to small-scale downwellings. Hence, both areas where material is partially molten and the location of the upwellings themselves have a much shorter wavelength and change much faster over time in comparison to the model without melt migration.
Fig. 114 Evolution of the model without (left) and with (right) melt migration.#
Fig. 114 shows the time evolution of both models. A more complete comparison of the two models can be found in Section 4.7 “Influence of melt migration on a global-scale convection model” in Dannberg and Heister [2016]).