Melt migration in a 2D mid-ocean ridge model#
This section was contributed by Juliane Dannberg.
The following cookbook will explain how to set up a model of a mid-ocean ridge that uses ASPECT’s implementation of coupled magma/mantle dynamics (see Section Calculations with melt transport) and melting and freezing of mantle rock. In particular, it will outline
how to use operator splitting to accurately compute melting and freezing of melt,
how to use traction boundary conditions to set up the flow field of a mid-ocean ridge,
useful strategies for how to refine the mesh in models with melt migration.
How to set up a model with melt migration in general is explained in the previous cookbook Melt migration in a 2D mantle convection model.
As the flow at mid-ocean ridges can be assumed to be roughly symmetric with respect to the ridge axis in the center, we only model one half of the ridge in a 2d Cartesian box with dimensions of \(105 \times 70\) km. Solid material is flowing in from the bottom with a prescribed temperature and melting due to decompression as is rises. The model is cooled from the top so that melt freezes again as it approaches this boundary. In addition, a fixed plate velocity away from the ridge axis is prescribed at the top boundary, inducing corner flow. Material can flow out freely at the right model boundary. The model shows both how melt is focused towards the ridge axis, and how melting and freezing induces chemical heterogeneity in the mantle, generating the crust and lithosphere. A movie of the full model evolution can be found online.
The input file#
One important problem in models with melting and freezing (and other reactions) is that these reactions can be much faster than the time step of the model. For mid-ocean ridges, melt is generally assumed to be in equilibrium with the solid, which means that the reaction is basically instantaneous. To model these type of processes, ASPECT uses operator splitting (see also Benchmarks for operator splitting): Reactions are solved on a different time scale than advection. For this model, this means that at the beginning of each time step, all melting reactions, including their latent heat effects, are solved using several shorter sub-time steps. In the input file, we have to choose both the size of these sub-time steps and the rate (or characteristic time scale) of melting, and they have to be consistent in the sense that the operator splitting time step can not be larger than the reaction time scale. The melting model we use here is the anhydrous mantle melting model of Katz et al. [2003] for a peridotitic rock composition, as implemented in the “melt simple” material model.
##################### Melting and freezing ########################
# Because the model includes reactions that might be on a faster time scale
# than the time step of the model (melting and the freezing of melt), we use
# the operator splitting scheme.
set Use operator splitting = true
subsection Solver parameters
subsection Operator splitting parameters
# We choose the size of the reaction time step as 200 years, small enough
# so that it can accurately model melting and freezing.
set Reaction time step = 2e2
# Additionally, we always want to do at least 10 operator splitting time
# steps in each model time step, to accurately compute the reactions.
set Reaction time steps per advection step = 10
end
end
# We use the melt simple material model that includes melting and freezing of
# melt for an average mantle composition that is characteristic for a mid-ocean
# ridge setting, and mainly use its default parameters.
# In particular, we have to define how fast melting and freezing should be.
# We assume that both reactions happen on a time scale of 200 years (or a rate
# of 5e-3/year), which should be substantially shorter than the time step size,
# so that the melt fraction will always be close to equilibrium.
# As the model includes melting and freezing, we do not have to extract any melt.
subsection Material model
set Model name = melt simple
subsection Melt simple
set Reference permeability = 1e-7
set Melt extraction depth = 0.0
set Freezing rate = 0.005
set Melting time scale for operator splitting = 2e2
end
end
To make sure we reproduce the characteristic triangular melting region of a mid-ocean ridge, we have to set up the boundary conditions in a way so that they will lead to corner flow. At the top boundary, we can simply prescribe the half-spreading rate, and at the left boundary we can use a free-slip boundary, as material should not cross this centerline. However, we do not know the inflow and outflow velocities at the bottom and right side of the model. Instead, what we can do here is prescribing the lithostatic pressure as a boundary condition for the stress. We accomplish this by using the “initial lithostatic pressure” model. This plugin will automatically compute a 1d lithostatic pressure profile at a given point at the time of the model start and apply it as a boundary traction.
##################### Velocity ########################
# To model the divergent velocitiy field of a mid-ocean ridge, we prescribe
# the plate velocity (pointing away from the ridge) at the top boundary.
# We use a closed boundary with free slip conditions as the left boundary, which
# marks the ridge axis and also acts as a center line for our model, so that
# material can not cross this boundary.
# We prescribe the velocity at the top boundary using a function:
# At the ridge axis, the velocity is zero, at a distance of 10 km from the ridge
# axis or more, the rigid plate uniformly moves away from the ridge with a constant
# speed, and close to the ridge we interpolate between these two conditions.
subsection Boundary velocity model
set Prescribed velocity boundary indicators = top:function
set Tangential velocity boundary indicators = left
subsection Function
# We choose a half-spreading rate of u0=3cm/yr.
set Function constants = u0=0.03, x0=10000
set Variable names = x,z
set Function expression = if(x<x0,(1-(x/x0-1)*(x/x0-1))*u0,u0); 0
end
end
# We prescribe the lithostatic pressure as a boundary traction on
# the bottom and right side of the model, so that material can flow in and out
# according to the flow induced by the moving plate.
subsection Boundary traction model
set Prescribed traction boundary indicators = right:initial lithostatic pressure, bottom:initial lithostatic pressure
subsection Initial lithostatic pressure
# We calculate the pressure profile at the right model boundary.
set Representative point = 105000, 70000
end
end
Finally, we have to make sure that the resolution is high enough to model melt migration. This is particularly important in regions where the porosity is low, but still high enough that the two-phase flow equations are solved (instead of the Stokes system, which is solved if there is no melt present in a cell). At the boundary between these regions, material properties like the compaction viscosity may jump, and there may be strong gradients or jumps in some solution variables such as the melt velocity and the compaction pressure. In addition, the characteristic length scale for melt transport, the compaction length \(\delta\), depends on the porosity:
While the melt viscosity \(\eta_f\) is usually assumed to be constant, and the shear and compaction viscosities \(\eta\) and \(\xi\) increase with decreasing porosity \(\phi\), the permeability \(k \propto \phi^2\) or \(k \propto \phi^3\) dominates this relation, so that the compaction length becomes smaller for lower porosities. As the length scale of melt migration is usually smaller than for mantle convection, we want to make sure that regions where melt is present have a high resolution, and that this high resolution extends to all cells where the two-phase flow equations are solved.
##################### Mesh refinement #########################
# We use adaptive mesh refinement to increase the resolution in regions where
# melt is present, and otherwise use a uniform grid.
subsection Mesh refinement
set Coarsening fraction = 0.5
set Refinement fraction = 0.5
# A refinement level of 5 (4 global + 1 adaptive refinements) corresponds to
# a cell size of approximately 1 km.
set Initial adaptive refinement = 1
set Initial global refinement = 4
set Strategy = minimum refinement function, composition threshold
set Time steps between mesh refinement = 5
subsection Minimum refinement function
set Coordinate system = cartesian
set Function expression = 4
set Variable names = x,y
end
# We use a very small refinement threshold for the porosity to make sure that
# all cells where the two-phase flow equations are solved (melt cells) have
# the higher resolution.
subsection Composition threshold
set Compositional field thresholds = 1e-6, 1.0
end
end
ASPECT also supports an alternative method to make sure that regions with melt are sufficiently well resolved, relying directly on the compaction length, and we will discuss this method as a possible modification to this cookbook at the end of this section.
The complete input file is located at cookbooks/mid_ocean_ridge/mid_ocean_ridge.prm.
Model evolution#
Fig. 115 Mid-ocean ridge model after 8 million years. The top panel shows the depletion and porosity fields (with the characteristic triangular melting region), the bottom panel shows the temperature distribution and the melt velocity, indicated by the arrows.#
When we look at the visualization output of this model (see also Fig. 115), we can see how the hot material flowing in from the bottom starts to melt as it reaches lower and lower pressures and crosses the solidus. Simultaneously, melting makes the residual solid rock more depleted (as indicated by the positive values of the compositional field called ‘peridotite’). Once material approaches the surface, it is cooled from the cold boundary layer above, and melt starts to crystallize again, generating ‘enriched’ basaltic crust where is freezes (as indicated by the negative values of the compositional field called ‘peridotite’). As the temperature gradients are much sharper close to the surface, this transition from melt to solid rock is much sharper than in the melting region. Once material crystallizes, it is transported away from the ridge axis due to the flow field induced by the prescribed plate velocity at the top boundary. This way, over time, the classical triangular melting region develops at the ridge axis, and the material transported away from the ridge shows two distinct layers: The top \(\approx 7\) km are enriched material, and form the basaltic crust (negative peridotite field), and the \(\approx 50\) km below are depleted material, and form the lithosphere (positive peridotite field). A vertical profile at a distance of 80 km from the ridge axis showing this composition can be found in Fig. 116.
Fig. 116 Vertical profile through the model domain at a distance of 80 km from the ridge axis at the end of the model run, showing the distribution of depletion and enrichment as indicated by the peridotite field.#
Mesh refinement#
Another option for making sure that melt migration is resolved properly in the model is using a refinement criterion that directly relates to the compaction length. This can be done in the mesh refinement section of the input file:
subsection Mesh refinement
set Coarsening fraction = 0.5
set Refinement fraction = 0.5
# Note that we allow for more adaptive refinements than before, as only cells
# with a small compaction length will be marked for refinement (as opposed to
# all melt cells), and we want to properly resolve the compaction length.
set Initial adaptive refinement = 3
set Initial global refinement = 4
set Strategy = minimum refinement function, compaction length
set Time steps between mesh refinement = 5
subsection Minimum refinement function
set Coordinate system = cartesian
set Function expression = 4
set Variable names = x,y
end
# We want the cells to be 8 times smaller than the compaction length.
subsection Compaction length
set Mesh cells per compaction length = 8.0
end
end
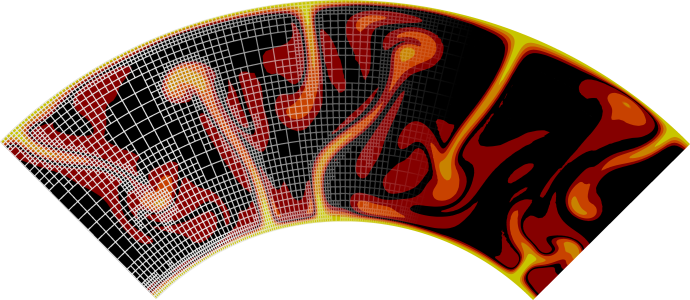
This will lead to a higher resolution particularly in regions with low (but not zero) porosity, and can be useful to resolve the strong gradients in the melt velocity and compaction pressure that are to be expected in these places (see Fig. 117). Of course it is also possible to combine both methods for refining the mesh.
Fig. 117 Mesh after a time of 3.6 million years for a model using the composition threshold refinement strategy (left) and the compaction length refinement strategy (right) Background colors indicate the melt velocity. Its sharp gradients at the interface between regions with and without melt can only be resolved using the compaction length refinement strategy.#
Extending the model#
There are a number of parameters that influence the amount of melting, how fast the melt moves, and ultimately the distribution of crustal and lithospheric material. Some ideas for adapting the model setup:
Changing the spreading rate: This can be done by choosing a different magnitude of the prescribed velocity at the top boundary, and influences the size and shape of the triangular melting region. Faster spreading allows hot material to move further away from the ridge axis, and hence facilitates a melting region that extends further in horizontal direction.
Changing the temperature profile: This can be done by choosing a different bottom boundary temperature and influences the amount of melting, and hence the thickness of the crust. Higher temperatures lead to more melt being generated.
Changing the speed of melt migration: The velocity of the melt with respect to the solid velocity is determined by the permeability and the melt viscosity (and the pressure gradients in the melt). Increasing the permeability (by setting a different “Reference permeability” in the melt simple model) can lead to higher melt velocities, melt reaching the depth of freezing faster, and hence lower overall porosity values at steady state.
Making the viscosity law more realistic: In this simple model, the viscosity only depends on the amount of melt that is present and is otherwise constant. This could be the reason why melt can not flow up all the way up at the ridge axis, but freezes before it reaches the surface. Introducing a temperature-dependent rheology could improve this behavior (and in reality, plastic effects might also play a role).