The 2D annulus benchmark#
This section was contributed by C. Thieulot, E. G. Puckett, and R. Gassmoeller.
This benchmark is based on a manufactured solution in which an analytical solution to the isoviscous incompressible Stokes equations is derived in an annulus geometry. The velocity and pressure fields are as follows:
with
The parameters \(A\) and \(B\) are chosen so that \(v_r(R_1)=v_r(R_2)=0\), i.e. the velocity is tangential to both inner and outer surfaces. The gravity vector is radial inward and of unit length.
The parameter \(k\) controls the number of convection cells present in the domain, as shown in Fig. 190 through Fig. 192.
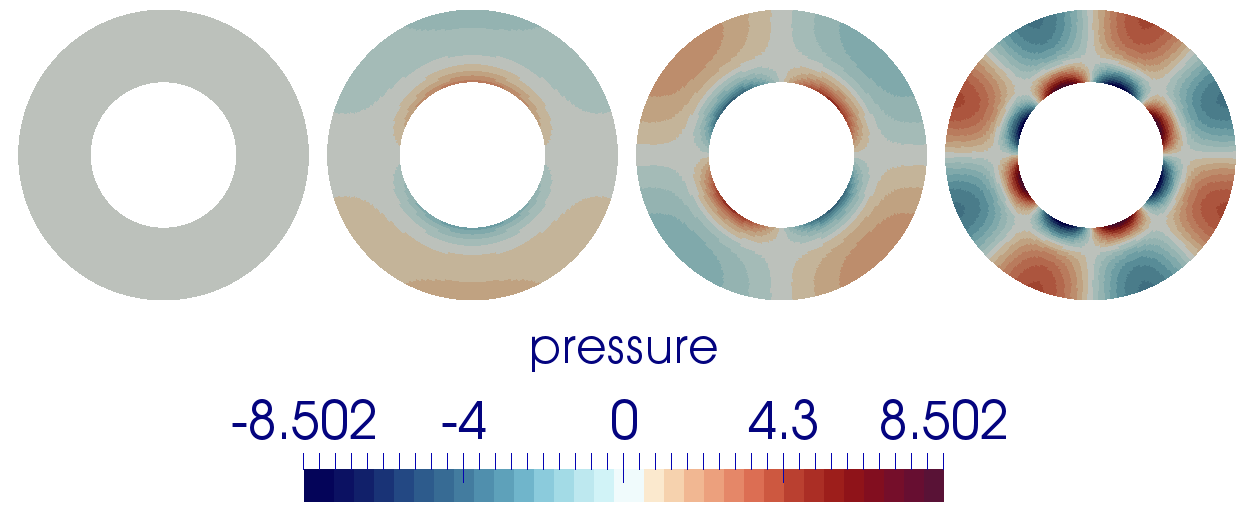
Fig. 190 Pressure fields for k=0,1,2,4 for the 2D annulus benchmark.#
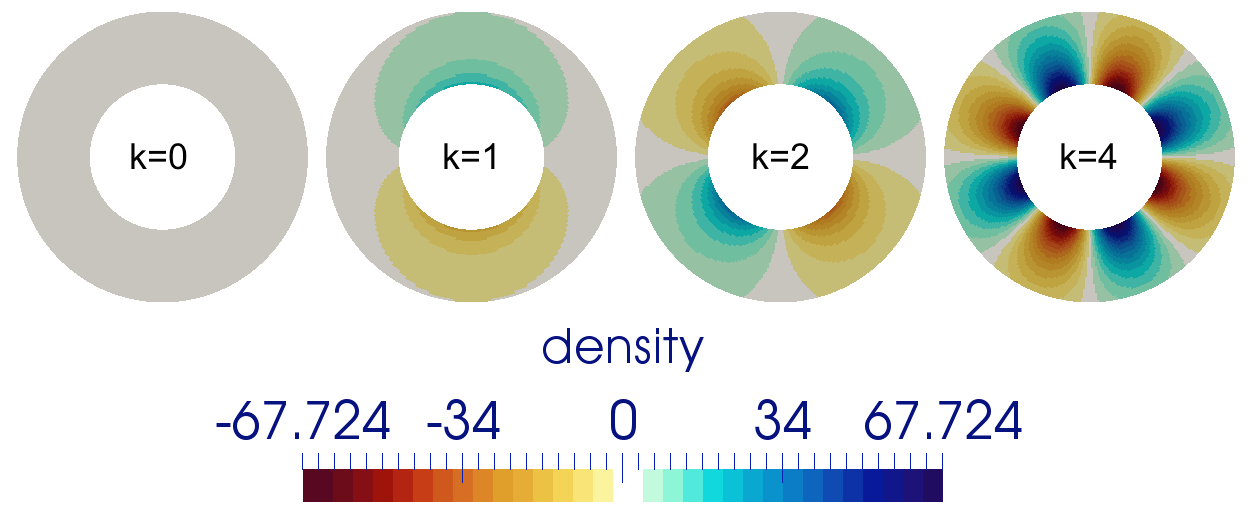
Fig. 191 Density fields for k=0,1,2,4 for the 2D annulus benchmark.#

Fig. 192 Velocity fields for k=0,1,2,4 for the 2D annulus benchmark.#
In the present case, we set \(R_1=1\), \(R_2=2\) and \(C=-1\). Fig. 193 shows the velocity and pressure errors in the \(L_2\)-norm as a function of the mesh size \(h\) (taken in this case as the radial extent of the elements). As expected we recover a third-order convergence rate for the velocity and a second-order convergence rate for the pressure.
Fig. 193 Velocity and pressure errors in the L2-norm as a function of the mesh size for the 2D annulus benchmark.#
Additionally, the subdirectory benchmarks/annulus/transient contains an extension of the benchmark to time-dependent flow. The benchmark and its results are described in Gassmöller et al. [2023], “Benchmarking the accuracy of higher order particle methods in geodynamic models of transient flow” see there for a detailed description.