Artificial viscosity smoothing
Artificial viscosity smoothing#
This section was contributed by Ryan Grove
Standard finite element discretizations of advection-diffusion equations introduce unphysical oscillations around steep gradients. Therefore, stabilization must be added to the discrete formulation to obtain correct solutions. In ASPECT, we use the Entropy Viscosity scheme developed by Jean-Luc Guermond and Richard Pasquetti and Bojan Popov [2011]. In this scheme, an artificial viscosity is calculated on every cell and used to try to combat these oscillations that cause unwanted overshoot and undershoot. More information about how does this is located at https://dealii.org/developer/doxygen/deal.II/step_31.html.
Instead of just looking at an individual cell’s artificial viscosity, improvements in the minimizing of the oscillations can be made by smoothing. Smoothing is the act of finding the maximum artificial viscosity taken over a cell \(T\) and the neighboring cells across the faces of \(T\), i.e.,
where \(N(T)\) is the set containing \(T\) and the neighbors across the faces of \(T\).
This feature can be turned on by setting the Use artificial viscosity smoothing
flag inside the Stabilization subsection inside the Discretization
subsection in your parameter file.
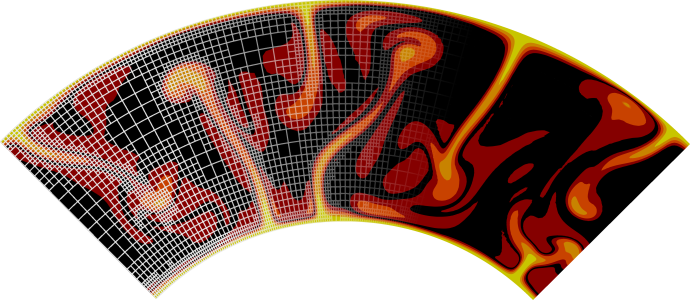
To show how this can be used in practice, let us consider the simple convection in a quarter of a 2d annulus cookbook in Section Simple convection in a quarter of a 2d annulus, a radial compositional field was added to help show the advantages of using the artificial viscosity smoothing feature.
By applying the following changes shown below to the parameters of the already existing file cookbooks/shell_simple_2d/shell_simple_2d.prm,
subsection Discretization
set Temperature polynomial degree = 2
subsection Stabilization parameters
set Use artificial viscosity smoothing = true
end
end
subsection Compositional fields
set Number of fields = 1
end
subsection Initial composition model
set Model name = function
subsection Function
set Variable names = x,y
set Function expression = if(sqrt(x*x+y*y)<4000000,1,0)
end
end
it is possible to produce pictures of the simple convection in a quarter of a 2d annulus such as the ones visualized in Figure Fig. 63.
Fig. 63 Example of the output of two similar runs. The run on the left has the artificial viscosity smoothing turned on and the run on the right does not, as described in Section Artificial viscosity smoothing.#