Layered flow with viscosity contrast
Layered flow with viscosity contrast#
This section was contributed by Cedric Thieulot.
The idea behind this benchmark is to construct an analytical solution to the incompressible Stokes equation in the case where the viscosity field showcases a viscosity contrast at location \(y=y_0\) whose amplitude and width can be controlled. The viscosity is defined as
where \(\beta\) and \(\epsilon\) are chosen by the user. Viscosity profiles for different values of \(\beta\) and \(\epsilon\) are shown in Fig. 184 and Fig. 185. The set up of this benchmark allows testing how discretizations deal with abrupt changes in the viscosity (if \(\beta\) is small) as well as large changes in the viscosity (if \(\epsilon\) is small).
Fig. 184 Layered flow benchmark: Viscosity profiles for various \(\beta\) values, using \(y_0 = 1/3\) and \(\epsilon = 0.0\).#
Fig. 185 Layered flow benchmark: Viscosity profiles for various \(\beta\) values, using \(y_0 = 1/3\) and \(\epsilon = 0.2\).#
The flow is assumed to take place in an infinitely long domain (in the horizontal direction) and bounded by \(y=-1\) and \(y+1\). At the bottom we impose \(v_x(y=-1)=0\), while we impose \(v_x(y=+1)=1\) at the top. The density is set to 1 while the gravity is set to zero. Under these assumptions, the flow velocity and pressure fields are given by:
where \(C_1\) and \(C_2\) are integration constants:
The viscosity and velocity fields are shown in Fig. 186 and Fig. 187 for \(\beta=0.01\) and \(\epsilon=0.05\).
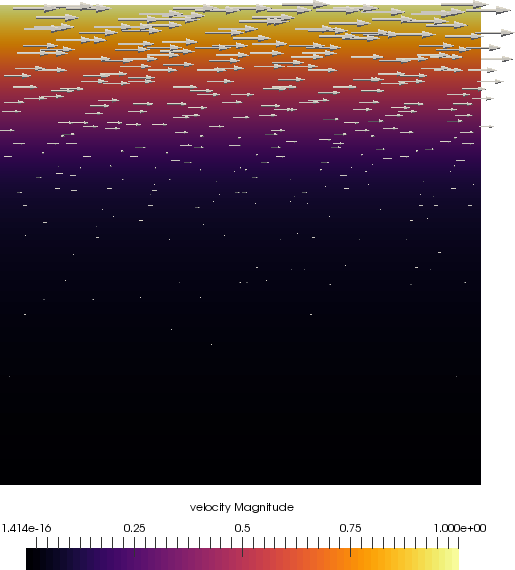
Fig. 186 Velocity fields for \(\beta=0.01\) and \(\epsilon=0.05\) at uniform level 8 resolution, using \(y_0=1/3\).#
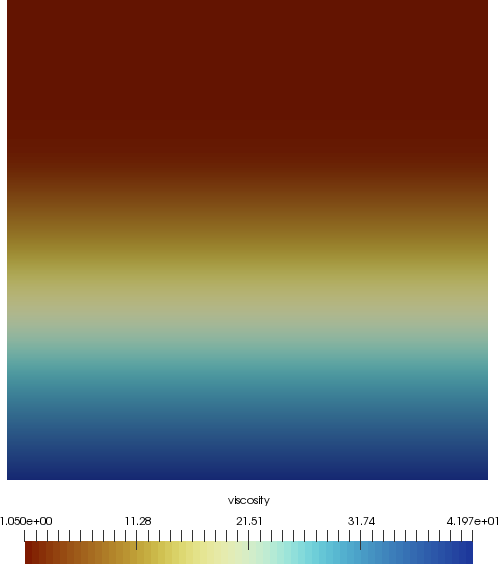
Fig. 187 Viscosity fields for \(\beta=0.01\) and \(\epsilon=0.05\) at uniform level 8 resolution, using \(y_0=1/3\).#