Kinematically-driven 2d oceanic subduction
Contents
Kinematically-driven 2d oceanic subduction#
This section was contributed by Anne Glerum.
This subduction example is based on the benchmark effort of Quinquis et al., of which initial results were published in Quinquis [2014]. In four increasingly complex setups we will go from isoviscous materials without any temperature effects to a fully thermo-mechanical, nonlinear, strain-weakened visco-plastic, externally-driven model of oceanic subduction. The setup of the most complex case is outlined in Fig. 109. The models are run for 15 My and slab tip depth, trench location, RMS velocity and temperature, and viscous dissipation are monitored. In addition, we discuss the effects of the element size of the subduction interface and crustal layers, viscosity averaging and the solver tolerance.

Case 1: Simple geometry and rheology#
The Case 1 model setup considers three materials (compositional fields) apart from the background sublithospheric mantle (see Fig. 110):
the lithosphere of the overriding plate (combining the BOC, SHB and thermal layer of the overriding plate in Fig. 109),
the crust of the subducting plate (weak seed and BOC combined), and
the mantle lithosphere of the subducting plate (SHB and thermal layer combined).
The geometry of these compositions is implemented as follows:
# We fix composition on the right boundary,
# because we have inflow there.
subsection Boundary composition model
set Fixed composition boundary indicators = right
set List of model names = initial composition
end
subsection Compositional fields
set Number of fields = 3
set Names of fields = OP, ML_SP, crust_SP
end
subsection Initial composition model
set List of model names = function
subsection Function
set Function constants = Ax=1475600.0, Az=670000.0, \
Bx=1500000.0, Bz=670000.0, \
Cx=1358500.0, Cz=588000.0, \
Dx=1382900.0, Dz=588000.0, \
Ex=1530000.0, Ez=560000.0, \
Fz=663000.0, Gz=662000.0, \
Hz=631000.0, Iz=630000.0
set Function expression = \
if(z>=Cz&z>=((Az-Cz)/(Ax-Cx)*(x-Cx)+Cz),1,0); \
if((x>=Ex&z>=Ez&z<Gz)|(x<Ex&z<=((Bz-Dz)/(Bx-Dx)*(x-Dx)+Dz)&z<Gz&z>=((Ez-Dz)/(Ex-Dx)*(x-Dx)+Dz)),1,0); \
if(z>=Cz&z>((Bz-Dz)/(Bx-Dx)*(x-Dx)+Dz)&z<((Az-Cz)/(Ax-Cx)*(x-Cx)+Cz)|z>=Gz&z<=((Bz-Dz)/(Bx-Dx)*(x-Dx)+Dz),1,0)
set Variable names = x,z
end
end
No differences in material properties exist, except for density and viscosity, so we use the multicomponent material model. To keep the boundaries between fields as sharp as possible in terms of viscosity, we use the maximum composition to determine the viscosity in each evaluation point (note that this can be harder on the solver):
set Nonlinear solver scheme = single Advection, single Stokes
subsection Material model
set Model name = multicomponent
subsection Multicomponent
set Reference temperature = 0.0
set Viscosity averaging scheme = maximum composition
# background, OP, ML SP, crust SP
set Viscosities = 1.e20, 1.e23, 1.e23, 1.e20
set Densities = 3200.0, 3250.0, 3250.0, 3250.0
set Thermal conductivities = 1
end
end
Temperature effects are ignored. Subduction is driven by prescribed in- and outflow through the right boundary (with a gradual transition of the flow direction), all other boundaries are free slip. The volume of material that flows in is balanced by the volume that is prescribed to flow out (this is important as the model is incompressible). A weak crust along the plate interface and the subducting lithosphere facilitates subduction. Through the function plugin, we prescribe the in- and outflow:
subsection Boundary velocity model
set Tangential velocity boundary indicators = left, bottom, top
set Prescribed velocity boundary indicators = right x:function
subsection Function
set Function constants = cm=100.0
set Function expression = if(z<540000.0, (600.0/550.0)/cm, \
if(z>560000.0, -5.0/cm, \
((((-600.0/550.0)-5.0)/-20.0)*((z/1000.0)-560.0)+5.0)*(-1.0/cm))); \
0
set Variable names = x,z
end
end
To follow the slab on its descent into the mantle, we use adaptive mesh refinement based on viscosity in combination with the minimum refinement strategy to ensure sufficient resolution in the crust and weak zone that allow the slab to detach from the surface:
subsection Mesh refinement
set Initial adaptive refinement = 2
set Initial global refinement = 8
set Minimum refinement level = 6
set Normalize individual refinement criteria = true
set Refinement criteria merge operation = plus
set Coarsening fraction = 0.01
set Refinement fraction = 0.95
set Run postprocessors on initial refinement = false
set Skip solvers on initial refinement = true
set Skip setup initial conditions on initial refinement = true
set Strategy = minimum refinement function, viscosity
set Time steps between mesh refinement = 16
subsection Minimum refinement function
set Coordinate system = depth
set Variable names = x,z,t
set Function constants = vel=150e3, L=100e3, crust=10e3
set Function expression = if(x<crust,10,if(x<L,9,if(x<vel,8,6)))
end
end
To monitor the model evolution, several diagnostic quantities are tracked over time: the depth of the tip of the slab, the position of the trench, the RMS velocity of the slab and the whole model domain, and the work done (viscous dissipation) in the slab and total model domain. The computation of these quantities in done in several new plugins:
subsection Postprocess
set List of postprocessors = visualization, velocity statistics, heating statistics, maximum depth of field, composition velocity statistics, viscous dissipation statistics
subsection Visualization
set List of output variables = density, viscosity, strain rate, error indicator
set Time between graphical output = 5e5
end
end

Fig. 110 Case 1 density, viscosity and velocity at time zero.#
We run the Case 1 setup for 15 My of model time. The diagnostic quantities in Fig. 111 show three stages of model evolution: first trench advance (top right plot), then free subduction (increasing slab RMS velocity), and after about 13 My interaction between the slab and bottom boundary at 660 km depth, which slows down the slab. The slab then curves inward along the bottom boundary. This can also be seen in Fig. 112.
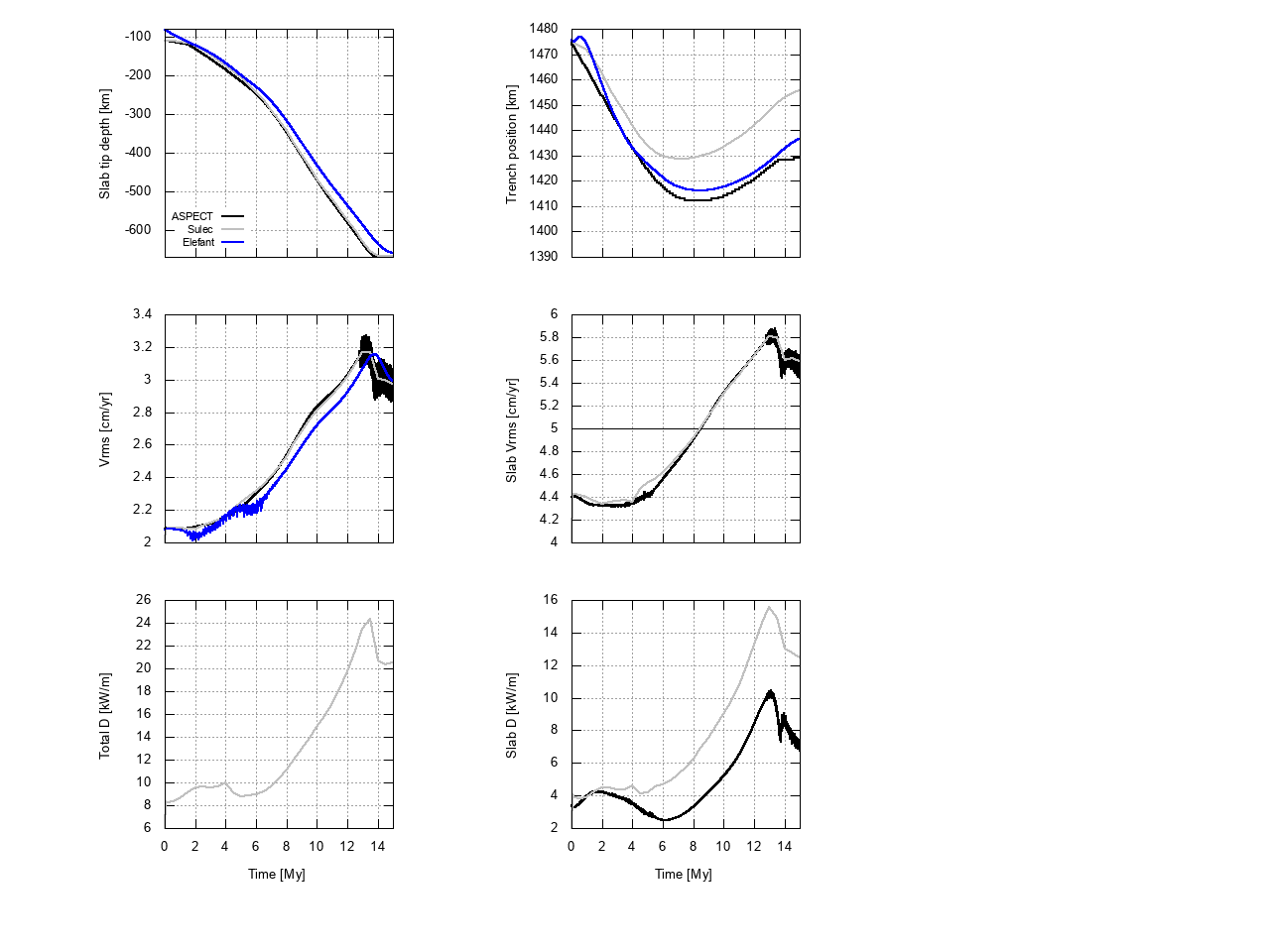
Fig. 111 Case 1 diagnostic quantities of ASPECT, Sulec and Elefant results.#

Fig. 112 Case 1 viscosity snapshots at 8 and 15 My.#